What are the different types of isoquants in production? Let’s look at some of the most popular isoquant types with the graphs.
Refer to the below article to gain a clearer understanding of isoquant curve analysis of production in economics.
Isoquant Curve Analysis of Production in Economics
Depending on the degree of substitutability of factors, the production isoquant can take on a variety of shapes. They are,
- Linear isoquant
- Input-output isoquant
- Kinked isoquant
- Smooth, convex isoquant
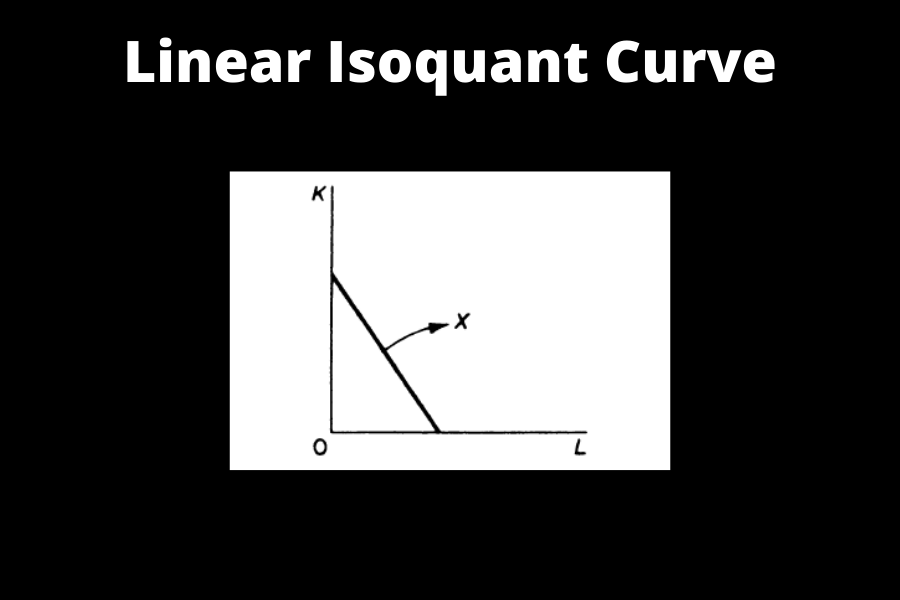
Types of Isoquants: Linear Isoquant
Linear isoquant assumes that all factors of production are perfectly substitutable. Given commodity may be produced using only capital, only labor, or an infinite mix of K and L.
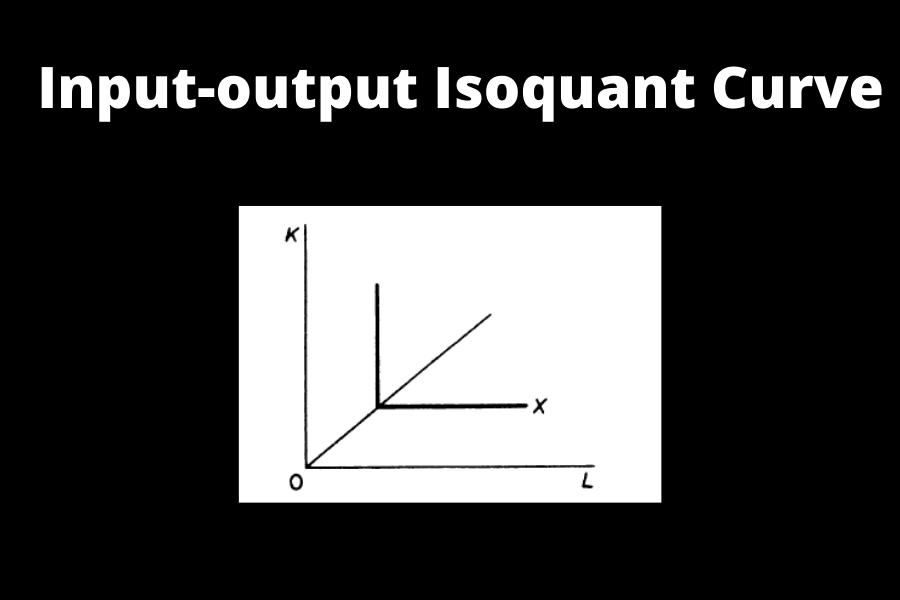
Types of Isoquants: Input-output Isoquant
Input-output Isoquant assumes that the factors of production are fully complementary (zero substitutability). For any commodity, there is only one method of production. A right angle is formed by the isoquant. This isoquant is also known as a ‘Leontief isoquant,‘ named after Leontief, the inventor of input-output analysis.
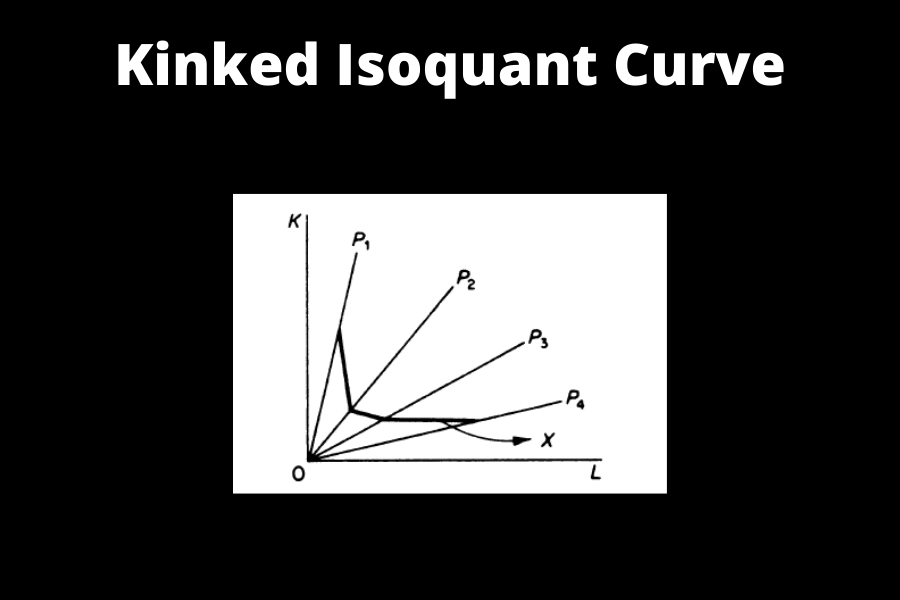
Types of Isoquants: Kinked Isoquant
The kinked isoquant assumes that K and L have limited substitutability. Each commodity is produced using only a few different processes. Only at the kinks is factor substitutability possible. This kind is also known as “activity analysis isoquant” or “linear programming isoquant” since it is mostly used in linear programming.
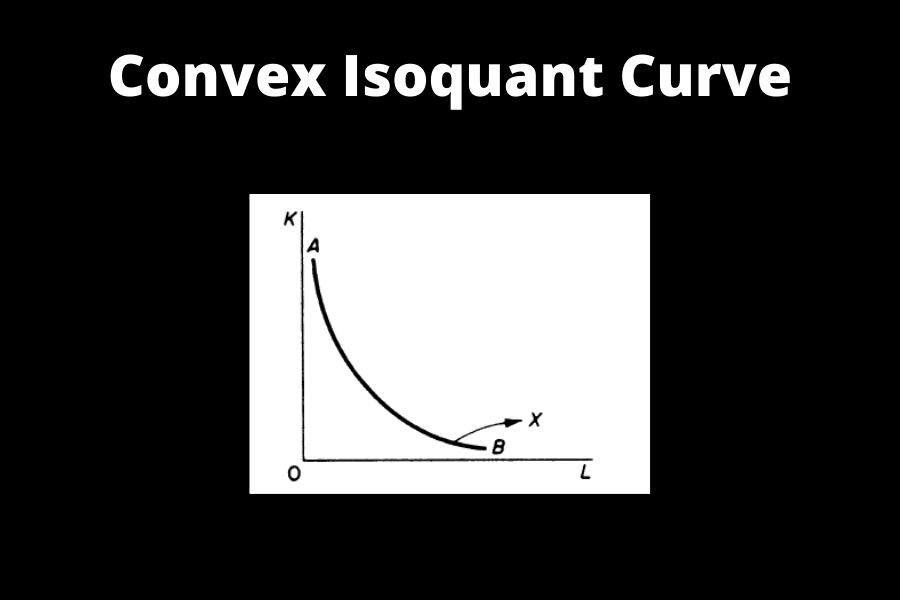
Smooth, convex Isoquant
This type assumes that K and L may be substituted continuously within a specified range, beyond which they can no longer be substituted. The isoquant is shown as a smooth curve that is convex to the origin.
Conclusion
- Kinked isoquants are more realistic.
- Traditional economic theory has chosen continuous isoquants because they are easier to handle using simple calculus methods.
- The continuous isoquant can be regarded as a simplified version to the more realistic form of a kinked isoquant.
- The kinked curve becomes closer and closer as the number of processes increases until the isoquant becomes a smooth curve at the limit (when the number of processes becomes infinite).
- The production function specifies not just one isoquant, but a whole variety of them, each with an unique output level. It illustrates how output varies as input factors change.
Did I miss anything?
Let me know by leaving a comment below right now.


